Personal Website of Moritz Lang

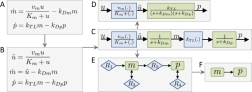
Relationship between modeling frameworks: A) ODEs; B-D) block-oriented nonlinear systems; E) species-reaction graph; and F) species-graph.

In systems and control theory, the problem at hand dictates the modeling framework, not vice versa. I thus dynamically iterate between models based on ordinary differential equations (ODE), stochastic models, graphs, block-oriented nonlinear systems, and others. The application of these frameworks to systems and control theory as well as my "inter-framework perspective" often results in interesting new theoretical approaches, which I subsequently generalize into consistent mathematical theories.

Relevant research: [Lang2009a, Lang2011a, Lang2014b, Lang2016c, Lang2016c, Lang2017a]

Imaging multiple fluorescence channels in parallel.

High quality modeling requires high quality data. Today, acquisition of such data is often rather hampered by software than by hardware capabilities. To improve the quality of my models, I thus support my experimental coworkers in providing software solutions for automated microscopy, microfluidic chip handling, cybergenetics, data analysis and similar.

Relevant research: [Lang2012a, Lang2018b]

Recently, I got interested in the Abelian sandpile. I showed that under harmonic fields, the sandpile identity shows harmonic dynamics smoothly transforming self-similar patterns onto one another. Thereby, the set of all harmonic fields provides universal coordinates for the sandpile group, allowing to map sandpile configurations between different domains. For more information, visit the project website.

Relevant research: [Lang2019a, Lang2019c]

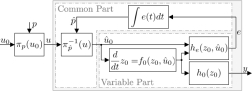
Scale-invariant networks can estimate the time-derivative of the logarithm of input signals, and are always implemented by means of an integral feedback.

Cells continuously estimate the state of the environment in order to adapt and to adjust their fate decisions. Often, the available information is incomplete or encoded into the environmental dynamics rather than the current environmental state. The facinating question how naturally evolved biomolecular networks then utilize regularities in environmental dynamics to estimate the current or future environmental conditions is one of my main research interests.

Relevant research: [Lang2016b, Barone2017, Lang2020a]

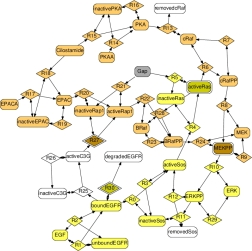
Modularization of the extracellular signal–regulated kinase (ERK) pathway model of Xu et al.(2010).

Most modularization approaches in biomolecular research focus on functional modules fulfilling specific biological tasks within the cell. In contrast, my research focuses on operational modules having no specific biological interpretation, but instead simplifying specic research tasks. For example, I developed modularization approaches to simplify parameter estimation, or to virtually insulate hypothesized network interactions from one another during their experimental validation.

Relevant research: [Lang2014a, Lang2014c, Prescott2015a, Lang2016c]

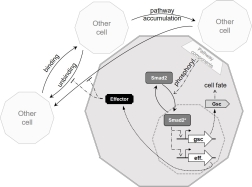
The cell fate decision in zebrafish gastrulation incorporates a kinetic proofreading mechanism measuring cell-cell contact durations.

In the mathematical modeling of biomolecular networks, I place special importance on understanding the biomolecular details of the modeled network as well as of the performed experiments. I take an active role by proposing experiments, questioning interpretations, requiring controls, or even getting my own hands "wet". Since the goal is never the model but always biological insight, I try to identify—by means of modeling—simple experiments conclusive even without the model.

Relevant research: [Bacchus2012b, Lang2016a, Barone2017, Pleska2018a, Lang2020a]